Frank Jin

Project 2: Fun With Frequencies

In this project, I play around the frequency space of images. You will see things such as, line detection, image sharpening, hybrid images, and multi-resolution blending.

Line detection

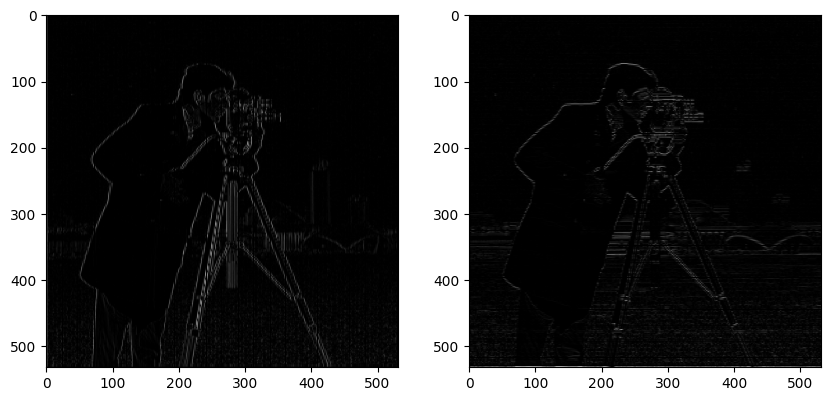
In this first section, I worked on image smoothing and sharpening. Starting with line detection, in the images below, I used two different types of filters. The Dx filter is a square matrix of [1, -1], while the Dy filter is a square matrix of [[1], [-1]]. Inverse to its name, the Dx filter approximates the derivative in the x direction, which in turns finds verticle lines. While the Dy filter does the same, but vertically, hence finding horizontal lines. You can see this when comparing to the original image. We can also try using percentile to try to clip to the lowest values of the line detection image. Although it needs manual adjustment, it works pretty well.

Original Cameraman Image

After applying Dx on the left, and Dy on the right.

Original Tobolsk Image

Moreover, we can also apply a gaussian blur to the image before hand as a low-pass filter, and getting rid of the highest frequencies. This will only leave more notable lines, efffectively eliminating noise. We can also combine the blurring and convolution of the Dx and Dy filters together, due to the commutive properties of convolution this will result in the same image.

Blurred Cameraman Image

Applying Dx and Dy to the blurred image.

The result of applying the combined blur and Dy Dx. The result is the same.

Image Sharpening

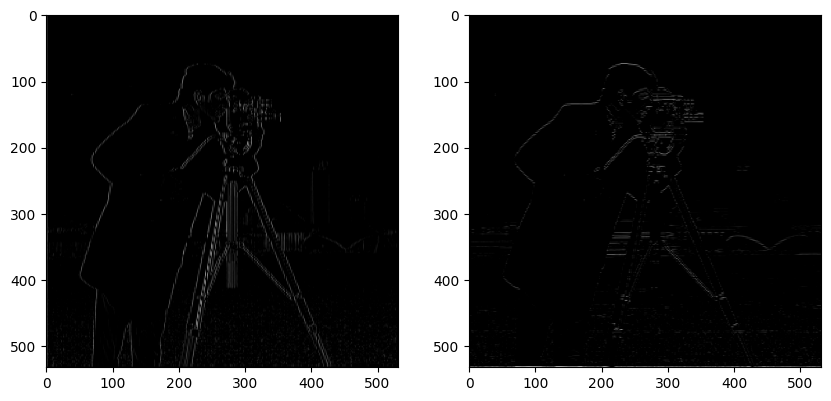
By the same principle of finding the lines in the image, which are the high frequency components of the image. We can also add them back into the original image, to achieve a sharpening effect. This will make the blurry parts of the image appear more distinct. Again we can also do this with a single convolution, by taking the image at each kernel, and subtracting away the a gaussian blurred version of the image. This is equivalent to adding the high frequency part.

Original Taj Image

Sharpened Taj Image

Original image of my younger brother kayaking.

Sharpened image of my younger brother kayaking.

Original image of UCB vs UCLA volleyball game.

Sharpened image of UCB vs UCLA volleyball game.

We can verify that this works by blurring a photo, and then sharpening it again. Suprisingly however, I noticed that the resharpened image does not seem to be the same quality. This may be because the image data is lost during gaussian convolution. As a result, it is not possible to recover the original image through this method.

Original garden image featuring grandfather!

Blurred garden image

Resharpened garden image

Hybrid Images

Another thing we can do with frequency manipulation is create hybrid images. These are images that are created using the low frequencies of one image, and the high frequencies of another. The result of combining the two is that we get an image that appears to be one thing from a distance, and another when up close.

Angry Person!

Happy?? Person

Angry from far away and Happy from up close!

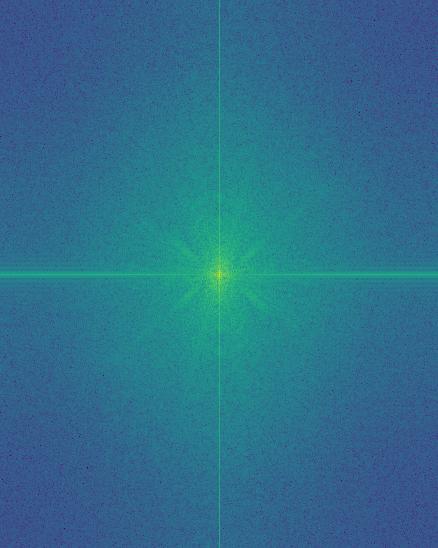
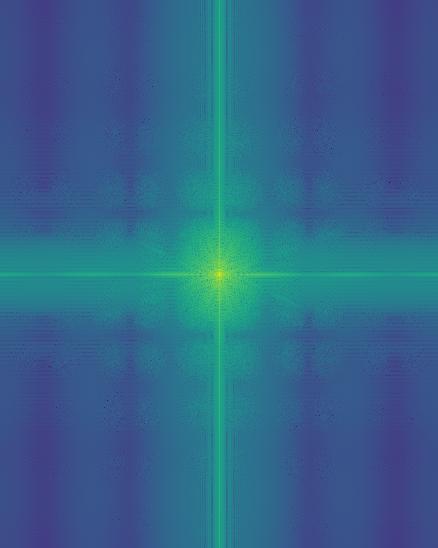
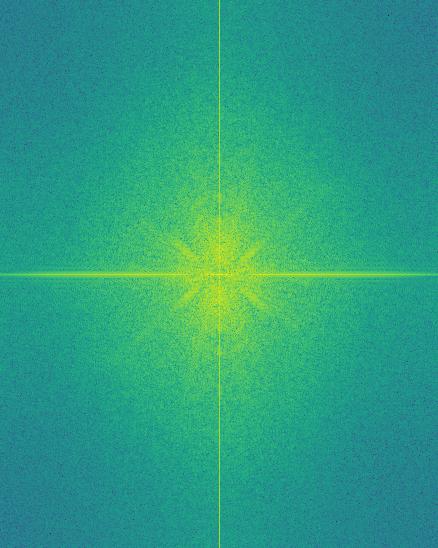
This is created by noticing taking the low pass and high pass of the images, then adding them together. We can also look at the FFT spectrum of the image, notice how the lines are quite distint. This allows the image to the distinguishable from each other.

FFT of Angry person

FFT of Happy person

FFT of the hybrid image

FFT of Angry person low passed

FFT of Happy person high passed

When using color it is best practice to color the low passed image, as colors are more recognizable from a distance. Also, it helps distinguish the low-pass image from far away. Where as coloring both, or coloring the high-pass image makes the images harder to seperate. A not so obvious failure is that if we color both images, then the colors will interfere with each other and make the resulting hybrid image very hard to distinguish. This is seen in one of the following examples. Another more obvious way of failure is trying to make a hybrid of two images that clearly done line up. This will also lead to poor results.

Colouring both images

Another example of colouring both images. This fails as the image interferes with each other.

Coloring only the high pass image

Coloring only the low pass image

As you can see, the low pass colored image is by far the best at all distances.

Multi-Resolution Blending

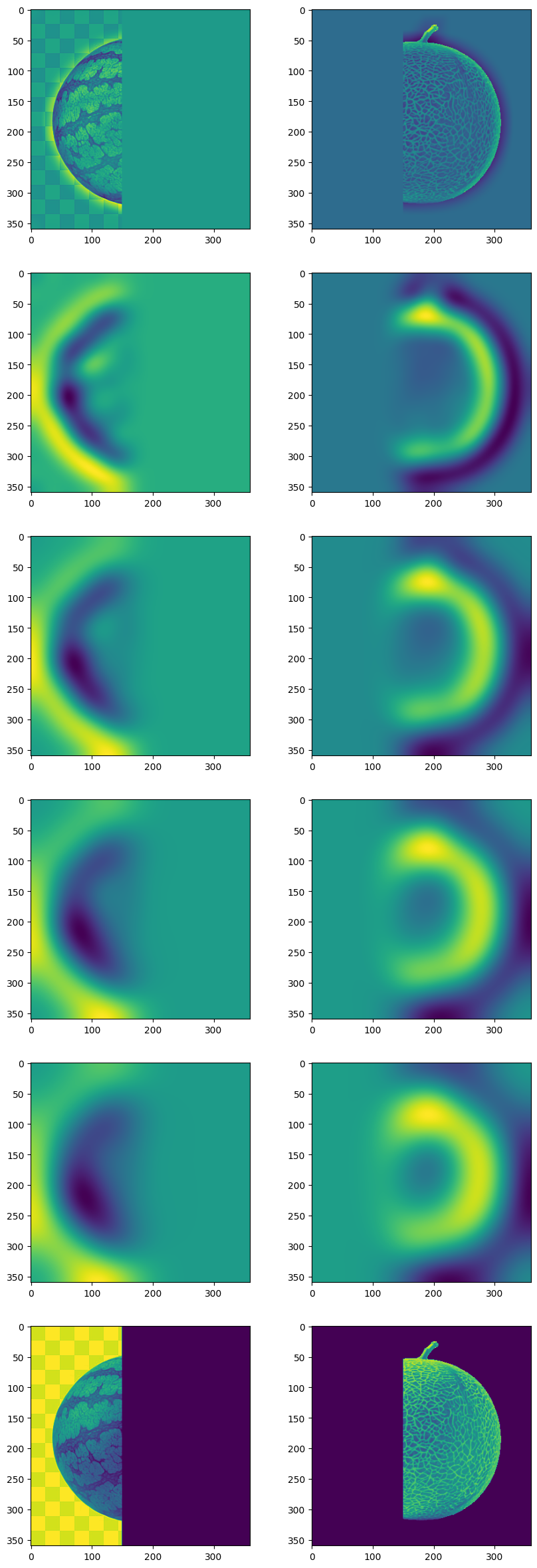
Going into the next part, we are trying to create images that can seamlessly blend into each other. We do this by creating a stack of laplacian filtered images. This creates a stack of images that decrease in frequency. In other words, this stack of images each represent some bandwith of frequencies that the images contain. By calculating this, adding a masking filter, and applying a gaussian over the masking filter, we can line up the bandwidths of two images, and merge them together. After all the layers of bandwidths have been added together, we can then sum up the stack, and add in the base gaussian.

The Laplace stack is calulated by first forming a gaussian stack. The gaussian stack is formed by taking a gaussian filter, and successively convoluting it with the image. The Laplace stack is the difference between each gaussian layer. An example is the oraple, which is shown below.